Резонансы в связанных контурах

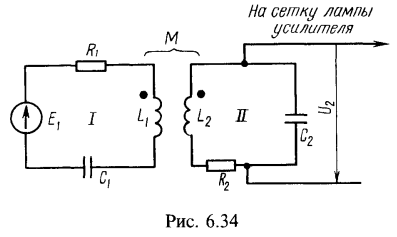
1. Антенный контур I (рис. 6.34) индуктивно связан с входным контуром II усилителя. Оба контура настроены в резонанс на частоту принимаемого сигнала . В антенном контуре наводится ЭДС , равная 100 мкВ. Дано: , коэффициент связи k=0,03.
Считая входное сопротивление усилителя бесконечным, определить: емкости , добротности каждого контура, взаимную индуктивность М, ток во втором контуре и напряжение на сетке входной лампы при частоте , частоты связи , ток и напряжение на сетке лампы при этих частотах; полосу пропускания индуктивно связанных контуров, сравнив ее с полосой пропускания каждого контура в отдельности.

Решение:
По условию имеем

отсюда

т. е. добротности контуров одинаковы.
Взаимная индуктивность

При расстройка , тогда учитывая, что фактор связи , найдем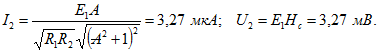
Частоты связи находим учитывая, что (в расчете использовано приближенное
соотношение при ):

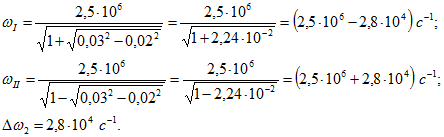
Обобщенная расстройка контуров при этих частотах

Ток и напряжение при частотах связи

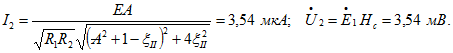
Относительную полосу пропускания для связи, больше критической :

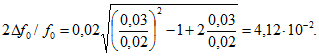
Она значительно превосходит относительную полосу пропускания одиночного контура:

2. Два одинаковых индуктивно связанных контура, параметры которых , настроены отдельно на одну и ту же частоту .
Определить: полосу пропускания каждого контура, полосу пропускания индуктивно связанных контуров при критической связи, максимальную полосу пропускания двух связанных контуров; при каких коэффициентах связи полоса пропускания двух связанных контуров будет:
а) в меньше, б) в 1,2 раза больше и в) в 2 раза больше по сравнению с полосой пропускания одиночного контура.

Решение:
Относительная полоса пропускания одиночного контура определяется затуханием контура.

тогда абсолютная полоса пропускания каждого контура

Относительную полосу пропускания двух индуктивно связанных контуров при критической связи рассчитывают

При этом абсолютная полоса пропускания

Максимальная полоса пропускания двух индуктивно связанных контуров:

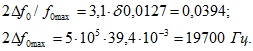
Для ответа на вопросы условия п. а и б данной задачи, условия которых соответствуют полосе пропускания при связи ниже критической, для которой :

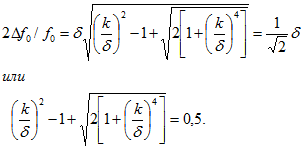
Решая последнее уравнение относительно k, найдем

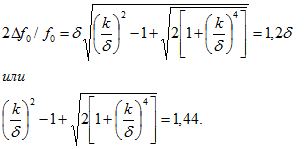
Решая эти уравнения относительно k, найдем
в) для ответа на вопрос п. в нужно воспользоваться формулой:

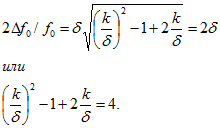
Решая последнее уравнение, найдем

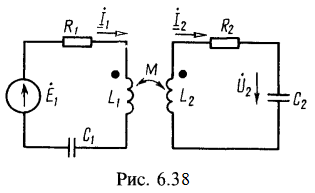
3. Система из двух одинаковых индуктивно связанных контуров, настроенных отдельно на частоту , имеет абсолютную полосу пропускания и взаимную индуктивность М=340 мкГн (см. рис. 6.38). Определить, какова связь между контурами (слабая, сильная или критическая) при . Найти коэффициент связи, индуктивность и резистивное сопротивление контуров для этих двух значений .

Решение:
Относительная полоса пропускания

Для того чтобы определить, какова связь между контурами, сравним , что соответствует критической связи. При этом .
Вычислим индуктивности контуров при .