Трансформаторные подстанции высочайшего качества

1. Приборы, подключенные к цепи (рис. 2.20), дали следующие показания: U=65 В, I=5 А, Р=300 Вт.
Вычислить комплексные сопротивления и проводимости цепи для случаев: .

Решение:
Модуль сопротивления и его аргумент определяют по формулам:

Искомые комплексные сопротивления и проводимости цепи:

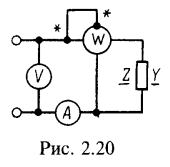
2. Комплексное напряжение и ток пассивного двухполюсника равны:

Вычислить комплексные сопротивление , проводимость и указать, каковы эквивалентные параметры двухполюсника. Чему равен сдвиг фаз между напряжением и током? Определить активную и реактивную составляющие напряжения и тока, активную, реактивную и полную мощности. Построить векторную диаграмму напряжений и токов.

Решение:
Запишем комплексные напряжение и ток в показательной форме и изобразим их на векторной диаграмме (рис. 2.21):

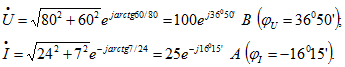
Определим комплексное сопротивление: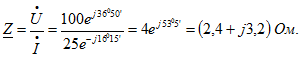

Следовательно, эквивалентными параметрами цепи являются резистивное R=2,4 0м и индуктивное сопротивления, соединенные последовательно.
Комплексную проводимость цепи определяют по формуле:

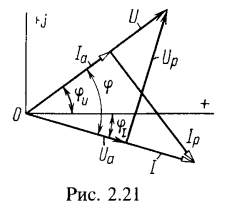
Эквивалентные параметры цепи: резистивная G=0,15 См и реактивная (индуктивная) В=0,2 См проводимости, соединенные параллельно.
Угол сдвига фаз между напряжением и током (он же аргумент )
Резистивные и реактивные составляющие напряжения и тока:

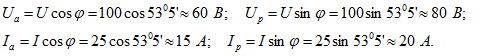
Необходимо обратить внимание на то, что вещественные и мнимые составляющие комплексных напряжения и тока в общем случае отличаются от их активных и реактивных составляющих.
Активная, реактивная и полная мощности:

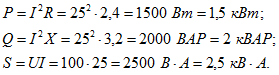
Те же мощности можно определить по формуле:

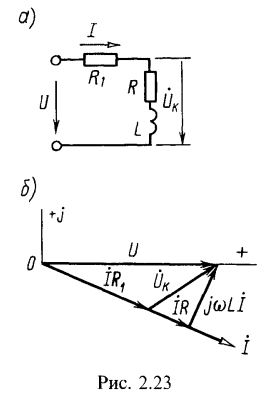
3. Последовательно с катушкой, параметры которой R=3 Ом, L=25 мГн, включен реостат сопротивлением (рис. 2.23, а). Определить напряжение на катушке , его сдвиг фазы по отношению к приложенному напряжению, а также мощность, расходуемую в катушке. К цепи подведено напряжение U=120 В, f=50 Гц. Построить векторную диаграмму напряжений и тока.

Решение:
Комплексное сопротивление всей цепи

Направим вектор U по оси вещественных чисел, т. е.
Комплексный ток

Напряжение на катушке

Оно сдвинуто по фазе по отношению к приложенному напряжению на угол . Векторная диаграмма приведена на рис. 2.23, б.
Мощность, расходуемая в катушке

Та же мощность может быть подсчитана и другим путем:

4. В цепи (рис. 2.31, в) дано: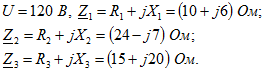

Определить токи активные и реактивные мощности всей цепи и отдельных ветвей. Построить векторную диаграмму.

Решение:
Полное сопротивление цепи:

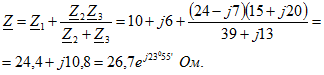
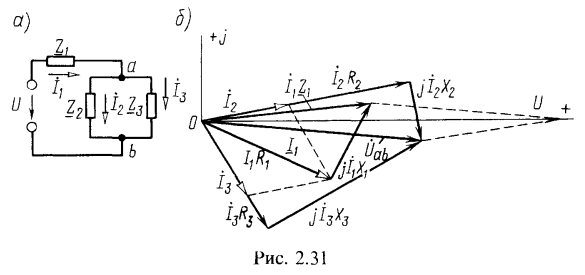
В неразветвленной части цепи проходит ток

Токи в параллельных ветвях могут быть выражены через ток в неразветвленной части цепи:

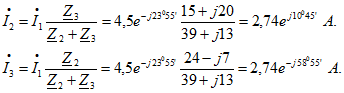
Токи можно найти и другим путем:

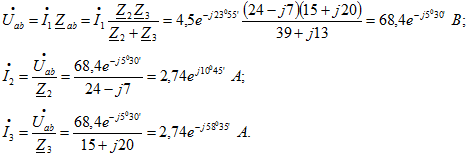
Найдем мощности (активные) всей цепи и отдельных ее ветвей:

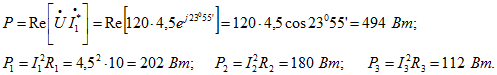
Проверка показывает, что .
Определим реактивные мощности всей цепи и отдельных ее ветвей:

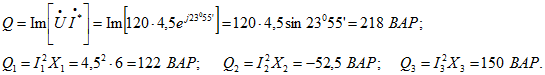
Учитывая, что реактивные мощности катушек положительны, а реактивная мощность конденсатора отрицательна, получим .
На рис. 2.31. б приведена векторная диаграмма. Порядок ее построения следующий: по результатам расчетов отложены векторы токов , затем по направлению отложен вектор и перпендикулярно ему в сторону опережения — вектор . Их сумма дает вектор . Далее в фазе с построен вектор и перпендикулярно ему в сторону отставания (так как отрицательно) вектор , а их сумма дает вектор напряжения на параллельном участке . Тот же вектор можно получить, если в фазе с отложить и к нему прибавить вектор опережающий на . Сумма векторов дает вектор приложенного напряжения.

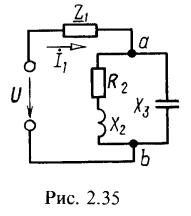
5. Параметры цепи (рис. 2.35): . Определить значение и характер сопротивления , если известно, что оно чисто реактивно и через него проходит ток , а напряжение, приложенное к цепи, .

Решение:
Сопротивление разветвленной части цепи

Общее сопротивление цепи . Оно может быть выражено и так: . Отсюда .
Возможны два решения задачи: искомое сопротивление имеет индуктивный характер и равно либо , либо .

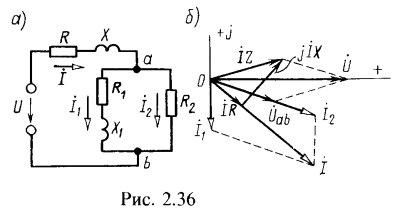
6. Каким резистивным сопротивлением следует зашунтировать сопротивление , чтобы ток, проходящий через , отставал от приложенного напряжения U на 90° (рис. 2.36, а)? Сопротивления: . Построить векторную диаграмму.

Решение:
Обозначим: тогда

Ток в неразветвленной части цепи

Через сопротивление проходит ток

Для того чтобы ток отставал по фазе от напряжения U на 90°, знаменатель последнего выражения должен быть чисто мнимым (по знаку положительным) значением.
Выпишем этот знаменатель и выделим в нем вещественную и мнимую составляющие

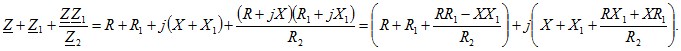
Вещественную часть полученного выражения приравняем нулю

отсюда

Векторная диаграмма представлена на рис. 2.36, б.

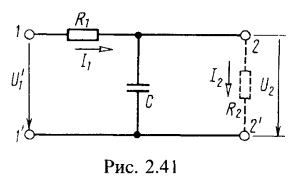
7. Вычислить резистивное сопротивление , которое надо подключить к зажимам 2—2′ цепи (рис. 2.41), чтобы отношение напряжения на этом сопротивлении к напряжению на входе цепи равнялось Н. Числовой расчет проделать при .

Решение:
Входное сопротивление всей цепи

где

Вычислим напряжение , для чего сначала найдем токи

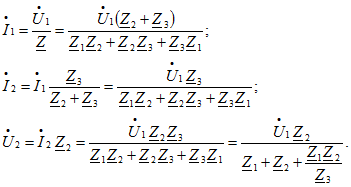
Отсюда определим отношение комплексных напряжений

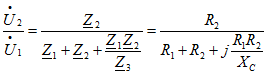
и отношение модулей напряжений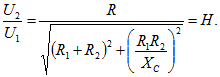

Подставляя числовые значения, после простых преобразований получим квадратное уравнение относительно .
Решение этого уравнения дает значение искомого сопротивления