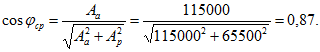Трансформаторные подстанции высочайшего качества

24. Батарея конденсаторов емкостью 10 мкФ соединена параллельно с реостатом, имеющим сопротивление r=318 Ом; схема включена на синусоидальное напряжение U=127 В частотой f=50 Гц.
Определить токи в ветвях батареи реостата, а также суммарный (неразветвленный) ток в цепи.

Решение:
Так как соединение параллельное, то напряжение 127 В приложено к обеим параллельным ветвям. Следовательно, на основании закона Ома ток в реостате

Так как при частоте 50 Гц емкостное сопротивление конденсатора емкостью 1 мкФ равно 3185 Ом, то у батареи емкостью 10 мкФ оно в 10 раз меньше, т. е.
Следовательно, ток в ветви батареи

Однако суммарный (неразветвленный) ток не будет равен арифметической сумме токов ветвей, т. е. 0,8 А.
Так как ток в реостате совпадает по фазе с напряжением, а ток в конденсаторе опережает по фазе напряжение на четверть периода, то векторы этих токов взаимно перпендикулярны, поэтому на основании теоремы Пифагора суммарный ток

Таким образом, токи параллельных ветвей, различно сдвинутые по фазе от общего напряжения этих ветвей, нельзя складывать так, как в цепи постоянного тока. Суммирование выполняют, учитывая расположение векторов относительно друг друга на векторной диаграмме. В частности, при двух токах параллельных ветвей, векторы которых взаимно перпендикулярны, суммарный ток можно определить, применив теорему Пифагора.

25. Параллельно включены активно-индуктивный приемник энергии, параметры которого , и чисто активный приемник сопротивлением .
Определить ток в подводящих проводах и сдвиг фаз этого тока относительно приложенного напряжения, если оно равно 220 В при частоте 50 гц.

Решение:
Индуктивное сопротивление первой параллельной ветви

Полное сопротивление этой ветви

Ток в первой параллельной ветви

Коэффициент мощности в этой ветви

Синус угла сдвига фаз для первой параллельной ветви

Активная составляющая тока в первой ветви

Реактивная составляющая тока в первой ветви

Ток во второй ветви, совпадающий по фазе с напряжением,

Этот ток арифметически сложим с активной составляющей тока в первой ветви. Получим активную составляющую суммарного (неразветвленного) тока:

Активная составляющая суммарного тока равна его реактивной составляющей:

Следовательно, этот ток отстает по фазе от приложенного напряжения на 1/4 периода:

Величина суммарного тока в раза больше каждой из его составляющих:

На рис. 29 дана векторная диаграмма, причем
Суммарный ток нельзя определить арифметическим сложением токов параллельных ветвей, так как это сложение дало бы

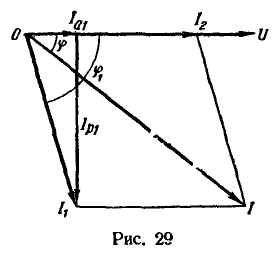
26. Параллельно соединены два активно-индуктивных приемника энергии. При напряжении 380 В и частоте 50 Гц первый приемник энергии имеет ток 50 А и активную мощность 15,2 кВт, второй приемник энергии — ток 25 А и мощность 5,7 кВт.
Определить суммарный ток в проводах линии и угол сдвига фаз между этим током и напряжением.

Решение:
Зная активную мощность и напряжение, можно определить активные составляющие тока приемника энергии:

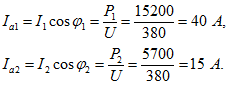
Активная составляющая суммарного тока равна арифметической сумме активных составляющих токов параллельных ветвей:

Этот ток можно определить иначе, если учесть, что при напряжении 380 В активная составляющая суммарного тока определяет суммарную активную мощность:

и, следовательно,

Полные мощности приемников энергии соответственно равны:

При различных углах сдвига фаз токов параллельных ветвей полная мощность всей установки не равна арифметической сумме полных мощностей ветвей.
Определяем реактивные мощности рассматриваемых активно-индуктивных приемников, учитывая, что активная, реактивная и полная мощности связаны между собой так же, как катеты и гипотенуза в прямоугольном треугольнике:

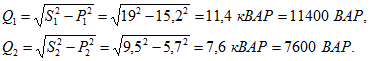
Так как токи обеих ветвей отстают по фазе от напряжения, то для получения суммарной реактивной мощности можно сложить арифметически реактивные мощности ветвей:

Полная мощность установки

Суммарный ток

Коэффициент мощности всей установки

Из таблиц тригонометрических величин .

27. Конденсатор емкостью 79,62 мкФ соединен последовательно с катушкой, параметры которой: r= 11 Ом и L=127,39 мГн.
Определить ток и напряжение на конденсаторе и на катушке при переменном напряжении между входными зажимами 121 В и частотах 50, 25 и 100 Гц.

Решение:
При частоте емкостное сопротивление конденсатора

Индуктивное сопротивление катушки при этом

Результирующее реактивное сопротивление при частоте 50 Гц в цепи отсутствует:

Следовательно, полное сопротивление цепи равно чисто активному сопротивлению:

Ток в цепи при резонансе максимален и равен

так как ограничивается только активным сопротивлением цепи.
Напряжение на конденсаторе

Напряжение на индуктивности равно емкостному напряжению:

Полное сопротивление катушки

Напряжение на катушке

При резонансе напряжений напряжения на конденсаторе и на катушке во много раз могут превышать приложенное напряжение. Так как при этом ток I=U/r, то

т. е. кратность превышения приложенного напряжения равна отношению реактивного (соответственно катушки и конденсатора) и активного сопротивлений цепи. В данном примере

Действительно,

При таком соотношении сопротивлений резонанс напряжений, наступивший неожиданно (когда класс изоляции не соответствует возникшему напряжению), может привести к пробою междувитковой изоляции и диэлектрика конденсатора. Это опасное последствие.
Однако радиотехника использует явление резонанса. Так называемая настройка радиоприемника на какую-либо станцию означает получение в колебательном контуре этого приемника условий резонанса с электромагнитными колебаниями, излучаемыми антенной радиостанции.
Резонансную частоту можно определить из условий резонанса напряжений в неразветвленном колебательном контуре:

откуда

или

Наконец,

В данном примере

При частоте , вдвое меньшей частоты 50 Гц, индуктивное сопротивление будет в 2 раза меньше , так как оно прямо пропорционально частоте; напротив, емкостное сопротивление будет в 2 раза больше .
Вследствие преобладания емкостного сопротивления над индуктивным в цепи будет наблюдаться режим тока, опережающего по фазе напряжение. Угол сдвига фаз

Из таблиц тригонометрических .
Полное сопротивление цепи

Ток в цепи на основании закона Ома

Величина этого тока в 5,5 раза меньше максимально возможного значения тока при данном напряжении, т. е. тока при резонансе напряжений.
Соответственно меньшему значению тока и большему значению емкостного сопротивления напряжение на конденсаторе будет равно

Напряжение на индуктивности

Напряжение на активном сопротивлении

Напряжение между зажимами катушки можно определить по его составляющим:

Полное сопротивление катушки

Напряжение катушки на основании закона Ома

Таким образом, состояние резонанса отличается большими значениями как тока, так и напряжений на отдельных элементах цепи. При частоте , вдвое большей частоты 50 Гц, индуктивное сопротивление катушки увеличится в 2 раза, так как оно прямо пропорционально частоте:

Напротив, емкостное сопротивление конденсатора, обратно пропорциональное частоте, при этом уменьшится вдвое и составит

Результирующее реактивное сопротивление носит индуктивный характер.
Ток в контуре будет отставать по фазе от напряжения, причем

Из таблиц тригонометрических величин .
Ток в цепи на основании закона Ома

где полное сопротивление цепи

Следовательно,

Напряжение на конденсаторе

Напряжение на индуктивности

Напряжение на активном сопротивлении

Напряжение катушки

где полное сопротивление катушки

Следовательно,

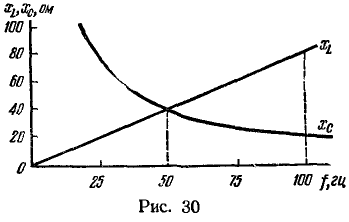
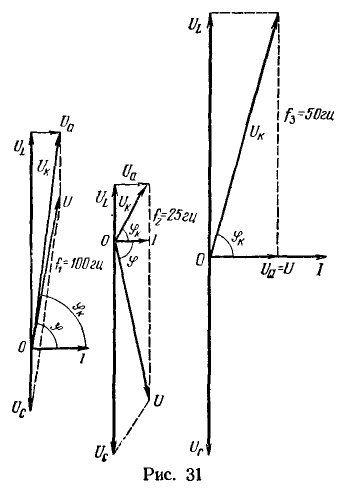
Покажем на графике изменение индуктивного сопротивления катушки и емкостного сопротивления конденсатора при изменении частоты (рис. 30). Кроме того, построим векторные диаграммы для режимов при частотах 50, 25 и 100 Гц (рис. 31). Примем масштабы: для режима при частоте 50 Гц и для двух остальных режимов.
Масштабы для токов взяты одинаковыми, поэтому длины отрезков, изображающих векторы токов, можно сравнивать между собой, не учитывая масштаба.
Чтобы по длинам векторов напряжений судить о соотношении между напряжениями в разных режимах (при различных частотах), следует длины указанных векторов из диаграмм для уменьшить в 2,5 раза и лишь после этого сравнивать их с длинами из диаграммы для .

28. Имеется конденсатор емкостью 50 мкФ и катушка индуктивностью 0,5 Гн.
Определить частоту, при которой наступит резонанс, в случае включения конденсатора и катушки последовательно. Какой должна быть емкость, чтобы при той же индуктивности резонанс наступил при частоте 50 Гц?

Решение:
При последовательном соединении катушки и конденсатора резонанс напряжений наступает, если индуктивное сопротивление равно емкостному:

откуда

Резонансная частота

При частоте 50 Гц угловая частота

Индуктивное сопротивление при этой частоте

Такую же величину должно иметь емкостное сопротивление:

откуда

29. При частоте f=50 Гц сопротивление катушки r=9 Ом, индуктивное сопротивление катушки , а емкостное сопротивление конденсатора, включенного, параллельно катушке, .
Определить токи в параллельных ветвях и суммарный ток, если приложенное напряжение U=380 В.

Решение:
Полное сопротивление катушки

Ток в ветви катушки

Активная составляющая тока катушки

Реактивная составляющая тока катушки

Сравним с этой составляющей тока катушки ток конденсатора, также чисто реактивный, но опережающий по
фазе напряжение на 1/4 периода:

Результирующий реактивный ток установки

Сравним величины результирующего реактивного тока и активного тока установки (он равен ):

Это отношение равно тангенсу угла сдвига фаз суммарного тока относительно напряжения:

Из таблиц тригонометрических величин .
Отсюда следует, что

Суммарный ток I, проходящий в проводах установки, определится как гипотенуза прямоугольного треугольника, одним из катетов которого является ток и другим — ток :

Здесь суммарный ток двух параллельных ветвей меньше каждого из них, тогда как в цепи постоянного тока суммарный ток равен арифметической сумме токов параллельных ветвей. Арифметическая сумма этих токов

более чем в 3,5 раза больше действительного суммарного тока, равного 4,072 А.

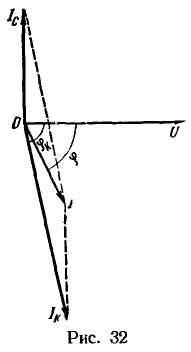
Проиллюстрируем расчет на векторной диаграмме, выбрав следующие масштабы: (рис. 32).
Из диаграммы видно, что в цепи с одной катушкой ток больше, чем после включения конденсатора параллельно катушке.
Помимо уменьшения тока по величине, он меньше сдвинут по фазе относительно напряжения. Если для катушки

то для схемы параллельного соединения катушки и конденсатора

Необходимо отметить, что присоединение конденсатора параллельно катушке не изменяет режима ее работы: остаются без изменения и, следовательно, . Конденсатор — чисто реактивный элемент цепи и потребление энергии после его присоединения не увеличивается.
Напротив, суммарный ток меньше тока катушки, поэтому при его прохождении в подводящих проводах, трансформаторе и генераторе потери энергии меньше, чем прежде.
Таким образом, целесообразно включение конденсатора параллельно активно-индуктивному приемнику энергии с целью уменьшения тока в проводах линии.

30. Катушка без стального сердечника и конденсатор соединены параллельно, причем колебательный контур настроен в резонансе с частотой сети.
Определить активную мощность катушки, если ее сопротивление r= 1 Ом, ток в конденсаторе и суммарный ток I= 1,1 А.

Решение:
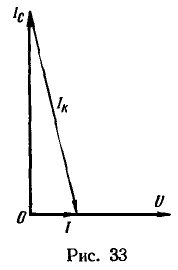
Если контур, описанный в условии задачи, настроен в резонанс, то векторная диаграмма цепи имеет вид, изображенный на рис. 33. Диаграмма построена в масштабе .
Как видно из рисунка, «треугольник векторов токов» прямоугольный, и по теореме Пифагора

В катушке происходит необратимое превращение электрической энергии в тепловую форму, поэтому активная мощность катушки

31. Катушка и конденсатор включены параллельно, причем при данной частоте в ветви катушки , а в ветви конденсатора .
Определить суммарный (неразветвлениый) ток, если приложенное напряжение U=220 В.

Решение:
Полное сопротивление в первой ветви

Полное сопротивление во второй ветви

Равенство полных сопротивлений параллельных ветвей означает равенство токов в этих ветвях:

Однако нельзя говорить о полной тождественности этих токов. Ток в первой ветви отстает по фазе от напряжения:

Ток во второй ветви опережает по фазе напряжение:

Так как эти углы примыкают на диаграмме друг к другу и произведение тангенсов этих углов равно единице:

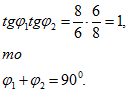
и токи взаимно перпендикулярны (рис. 34).
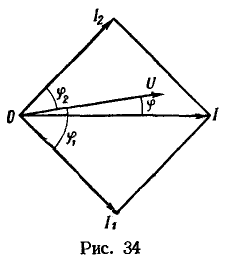
Суммарный ток

32. В цехе установлены 30 одинаковых однофазных электродвигателей, каждый из которых имеет мощность 0,38 кВт при потреблении энергии от сети и работает при среднем . Коэффициент одновременной работы электродвигателей равен 0,95.
Какой емкости батарею конденсаторов следует включить параллельно сети электродвигателей, чтобы повысить установки до 0,885, если подводимое напряжение U = 380 В и частота f=50 Гц?

Решение:
Активная мощность одновременно работающих электродвигателей при потреблении энергии от сети

Активная составляющая суммарного тока одновременно работающих электродвигателей

Тангенс угла сдвига фаз, соответствующий значению коэффициента мощности, определяем по таблицам тригонометрических величин:

Реактивная составляющая суммарного тока одновременно работающих электродвигателей

В результате включения батареи конденсаторов электродвигатели будут попрежнему иметь активную мощность 10,83 кВт и прежнюю активную составляющую суммарного тока, т. е. . Соответственно новому значению Коэффициента мощности реактивная составляющая суммарного тока будет менее 27,8 А (из таблиц тригонометрических величин ).
Следовательно,

Уменьшение реактивной составляющей суммарного тока происходит вследствие компенсации ее емкостным током конденсаторов.
Из соотношения токов

следует после подстановки, что

Емкостное сопротивление батареи конденсаторов

Емкость

Если проследить весь ход выполненного расчета, то можно сделать вывод, что емкостный ток конденсаторов должен быть равен разности двух реактивных составляющих токов установки:
до компенсации

после компенсации

Здесь — активная составляющая тока установки, не зависящая от включения устройств, компенсирующих сдвиг фаз.
Таким образом,

откуда емкость конденсаторов

Из этой формулы следует, что емкость батареи конденсаторов при данной реактивной мощности обратно пропорциональна квадрату напряжения. Поэтому при компенсации сдвига фаз в цепи высокого напряжения требуется меньшая емкость, чем в цепи низкого напряжения.

33. Коэффициент мощности приемника энергии повышают с 0,7 до 0,91. Потери мощности в линии передачи равны 8% от мощности приемника (при ).
На сколько процентов можно увеличить активную мощность при передаче энергии с той же потерей мощности в линии, но при повышении до 0,91 и сколько процентов будут составлять потери мощности, если активную мощность приемника не увеличивать?

Решение:
Потери мощности в линии останутся прежними:

если суммарный ток I приемников энергии останется прежним (r — сопротивление проводов линии).
Этот ток можно выразить из формулы мощности:

где индекс 1 относится к режиму до компенсации, а индекс 2 — к режиму после повышения коэффициента мощности.
Отсюда видно, что после повышения мощность приемника может иметь значение

т. е. активную мощность приемника можно увеличить на 30% путем присоединения новых приемников энергии. Если активную мощность приемника оставить прежней:

то в результате повышения коэффициента мощности ток в проводах линии уменьшится.
Действительно, из последнего выражения

В формулу потери мощности в линии этот ток входит в квадрате: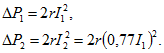

Потери мощности в линии составят от прежней величины

поэтому

34. За месяц работы завода показания счетчиков активной энергии увеличились на , а счетчики реактивной энергии зарегистрировали за то же время .
Определить среднемесячный коэффициент мощности.

Решение:
Счетчики активной и реактивной энергии были включены в одно и то же время. Отношение реактивной и активной энергии равно среднемесячному тангенсу угла фаз. Действительно,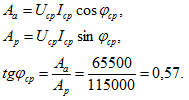


Следовательно,

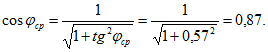
Среднемесячный коэффициент мощности можно определить также по формуле