Однофазные цепи переменного тока (страница 2)
12. Конденсатор емкостью С = 8,36 мкФ включен на синусоидальное напряжение U=380 В частотой f=50 Гц.
Определить ток в цепи конденсатора.
Решение:
Емкостное сопротивление
Ток в цепи конденсатора при синусоидальном напряжении 380 В
Для получения больших токов требуются при данной частоте большие значения емкости.
13. При включении конденсатора на синусоидальное напряжение U=220 В частотой f=50 Гц в цепи установился ток I=0,5 А.
Какую емкость имеет конденсатор?
Решение:
На основании закона Ома емкостное сопротивление
Из формулы емкостного сопротивления 
емкость
Метод определения емкости конденсатора, рассмотренный в данной задаче, является наименее точным, но он прост и не требует больших затрат для применения на практике.
14. При включении разомкнутого на конце кабеля на напряжение U=6600 В частотой f=50 Гц в цепи установился ток I=2 А.
Пренебрегая электрическим сопротивлением кабеля, определить приближенно емкость кабеля на 1 км его длины, если длина кабеля 10 км.
Решение:
Изолированные друг от друга жилы кабеля представляют собой конденсатор. Если пренебречь сопротивлением жил кабеля, то ток холостой работы кабеля, т. е. ток в кабеле, разомкнутом на конце, можно считать чисто емкостным. В этом случае действительно соотношение
где 
— емкостная проводимость.
Отсюда
При частоте f=50 Гц угловая частота 
, следовательно,
Емкость кабеля на 1 км его длины
Описанный способ определения емкости кабеля на 1 км его длины является очень приближенным (в нем пренебрегают активным сопротивлением жил кабеля и активной проводимостью утечки от жилы к жиле вследствие несовершенства изоляции; допускается равномерное распределение емкости по длине кабеля).
15. Какая емкость батареи конденсаторов требуется для получения реактивной (емкостной) мощности 152 ВАР при напряжении U=127 В и частоте f=50 Гц.
Решение:
При частоте f=50 Гц угловая частота 
. Так как ток батареи считается чисто
реактивным (опережающим по фазе напряжение на 1/4 периода), то реактивная мощность равна произведению напряжения и тока:
откуда
Емкостный ток равен произведению напряжения на емкостную проводимость, поэтому
Емкость батареи конденсаторов
Реактивную (емкостную) мощность можно представить в виде 
, выразив ток через напряжение и емкостную проводимость; отсюда следует, что при данном напряжении и частоте реактивная (емкостная) мощность пропорциональна емкости. Если изоляция пластин батареи конденсаторов допускает повышение напряжения (например, в 
раз), то реактивная (емкостная) мощность увеличится пропорционально квадрату напряжения (т. е. в 3 раза). Таким образом, в рассматриваемом случае важное значение имеет отношение напряжения от номинального.
16. В катушке (см. задачу 10), включенной на переменное напряжение U=12 В частотой f=50 Гц установился ток 1,2 А.
Определить индуктивность катушки.
Решение:
Отношение переменного напряжения, приложенного к катушке, к току, устанавливающемуся в ней, называется полным сопротивлением z катушки;
В задаче 10 было определено, что активное сопротивление катушки r=2,8 Ом. Сопротивление катушки при перееденном токе больше сопротивления г при постоянном токе вследствие наличия э. д. с. самоиндукции, препятствующей изменению переменного тока. Это равносильно появлению в катушке сопротивления, называемого индуктивным:
где L — индуктивность, Гн
f — частота, Гц.
Связь между полным сопротивлением z, индуктивным сопротивлением 
и активным сопротивлением r такая же, как между гипотенузой и катетами в прямоугольном треугольнике:
откуда индуктивное сопротивление
Индуктивность катушки
В рассматриваемой катушке ток отстает по фазе от напряжения, причем тангенс угла сдвига фаз 
. Из таблиц тригонометрических величин 
.
17. В схеме (рис. 23) вольтметр показывает 123 В, амперметр 3 А и ваттметр 81 Вт, частота сети 50 Гц.
Oпределить параметры катушки.
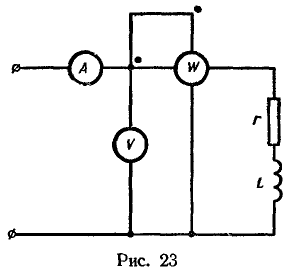
Решение:
Отношение напряжения к току равно полному сопротивлению катушки:
Ваттметр измеряет активную мощность цепи, которая в данной задаче является потерей мощности в сопротивлении r, поэтому сопротивление катушки
Полное сопротивление z, активное сопротивление r и индуктивное сопротивление 
катушки связаны между собой таким же соотношением, как гипотенуза и катеты в прямоугольном треугольнике.
Следовательно,
При частоте f=50 Гц угловая частота
Индуктивное сопротивление 
равно произведению угловой частоты ω и индуктивности L; следовательно,
Коэффициент мощности катушки 
. Из таблиц тригонометрических величин 
.
18. Катушка без стального сердечника включена на постоянное напряжение 2,1 В, ток которой равен 0,3 А. При включении этой же катушки на синусоидальное напряжение частотой 50 Гц с действующим значением 50 В ток имеет действующее значение 2 А.
Определить параметры катушки, активную и полную мощности.
Решение:
Отношение постоянного напряжения к постоянному току в катушке практически равно (если пренебречь увеличением сопротивления из-за вытеснения переменного тока на поверхность провода) активному сопротивлению:
Это один из параметров катушки. Отношение этих же величин при переменном токе в катушке равно полному сопротивлению:
Индуктивное сопротивление:
Индуктивность катушки — второй ее параметр:
Коэффициент мощности катушки:
Из таблиц тригонометрических величин 
.
Активная мощность
Полная мощность
Коэффициент мощности
В задачах 17 и 18 рассмотрены два различных способа определения параметров катушки.
19. Батарея конденсаторов емкостью С=50 мкФ соединена последовательно с реостатом сопротивлением r=29,1 Ом.
Определить напряжения на батарее конденсаторов и реостате, а также ток в цепи и мощность, если приложенное напряжение U=210 В и частота сети f=50 Гц.
Решение:
Частоте 50 Гц и емкости 50 мкФ соответствует емкостное сопротивление, в 50 раз меньшее, чем емкости в 1 мкФ. Следовательно,
Здесь 3185 Ом — сопротивление конденсатора емкостью 1 мкФ.
По условию, сопротивление реостата r=29,1 Ом. Полное сопротивление цепи связано с активным и емкостным сопротивлениями таким же соотношением, как гипотенуза и катет прямоугольного треугольника:
На основании закона Ома ток в цепи
Напряжение на реостате
Напряжение на батарее конденсаторов
В силу последовательного соединения большее напряжение оказалось на элементе цепи, имеющем большее сопротивление.
Коэффициент мощности
Из таблиц тригонометрических величин угол сдвига фаз 
.
Активная мощность цепи
Полная мощность цепи равна произведению действующих значений напряжения и тока:
Полная мощность намного больше активной мощности, так как коэффициент мощности мал, т. е. полное сопротивление цепи во много раз превышает активное сопротивление.
20. Электрическую лампу мощностью Р=60 Вт при напряжении 
необходимо подсоединить к сети с переменным напряжением U=220 В и частотой 50 Гц. Для компенсации части этого напряжения последовательно с лампой включается конденсатор.
Какой емкости необходимо взять конденсатор?
Решение:
Напряжение на лампе будет активной составляющей приложенного напряжения сети, а напряжение на конденсаторе — его реактивной (емкостной) составляющей. Эти напряжения связаны соотношением
Напряжение на конденсаторе
Ток в конденсаторе тот же, что и в лампе, т. е.
На основании закона Ома емкостное сопротивление
Так как при частоте f=50 Гц емкости С=1 мкФ соответствует емкостное сопротивление 
, то емкость рассматриваемого конденсатора приблизительно равна 8,7 мкФ.
Избыточное напряжение можно было бы скомпенсировать и путем последовательного включения реостата с лампой. Так как реостат, как и электрическая лампа, представляет чисто активное сопротивление, то напряжения на этих элементах цепи совпадают по фазе с общим током, а следовательно, и между собой. В этом случае будет действительно соотношение
где 
— напряжение на реостате, равное
При токе лампы 0,5 А сопротивление реостата должно составлять
В реостате будет расходоваться энергия, переходящая в тепло, причем потери мощности в реостате
В случае включения емкости «погашение» напряжения происходит без потерь энергии.
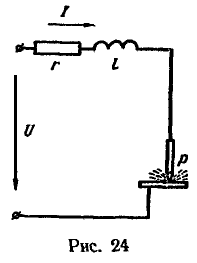
21. В случае электрической сварки дугой тонких листов при переменном токе в ней развивается мощность 
при токе I=20 A. Напряжение источника U=120 В, частота сети f=50 Гц (рис. 24). Чтобы иметь необходимое напряжение на дуге, последовательно с ней включили индуктивную катушку, сопротивление которой r=1 Ом.
Определить индуктивность катушки; сопротивление реостата, который можно было бы включить вместо катушки; к.п.д. схемы при наличии в ней катушки и реостата.
Решение:
Полное сопротивление схемы
Полная мощность на входе схемы
Потери мощности в обмотке катушки
Активная мощность схемы
Коэффициент мощности схемы
Из таблиц тригонометрических величин 
.
Активное сопротивление схемы
сопротивление дуги
Индуктивное сопротивление цепи представлено индуктивным сопротивлением катушки:
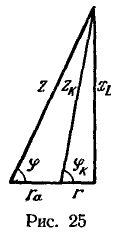Эту же величину можно определить из треугольника сопротивлении (рис. 25, масштаб 
)
Искомая индуктивность катушки
Если бы вместо катушки был включен реостат, то сопротивление схемы имело бы ту же величину 6 Ом, но было бы чисто активным:
откуда
Потери мощности в катушке
Потери мощности в реостате
Отсюда ясно, что к. п. д. схемы выше при «погашении» избытка напряжения индуктивной катушкой. Действительно, к. п. д. при наличии катушки
к. п. д. при наличии реостата
Не следует забывать, что «погашение» избытка напряжения катушкой (или конденсатором) ухудшает коэффициент мощности (в данном примере 
при наличии катушки и 
при наличии реостата).
22. Последовательно с катушкой, параметры которой 
и L=15,92 мГн, включен реостат сопротивлением, 
. Цепь включена на напряжение U=130 В при частоте f=50 Гц.
Определить ток в цепи; напряжение на катушке и реостате; коэффициент мощности цепи и катушки.
Решение:
Индуктивное сопротивление катушки
Полное сопротивление катушки
Активное сопротивление цепи, состоящей из последовательно соединенных катушки и реостата,
Полное сопротивление цепи
На основании закона Ома ток в цепи
Напряжение на катушке
Напряжение на реостате
Арифметическая сумма 
много больше приложенного напряжения U=130 В. Коэффициент мощности цепи
Коэффициент мощности катушки
Следовательно, реостат увеличивает коэффициент мощности и сопротивление цепи, но уменьшает ток, увеличивает потребление энергии схемой.
Действительно, активная мощность катушки
активная мощность реостата
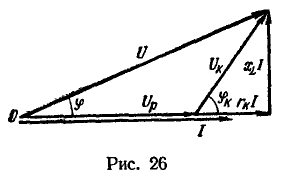Так как цепь неразветвленная и ток один, то с него целесообразно начать построение векторной диаграммы (рис. 26).
Напряжение на реостате, представляющем собой чисто активное сопротивление, совпадает по фазе с током; на диаграмме вектор этого напряжения совпадает по направлению с вектором тока. Из конца вектора 
в сторону опережения вектора тока I, под углом 
в сторону, противоположную вращению стрелки часов, откладываем вектор напряжения на катушке 
. Векторы 
построены так с целью сложения по правилу многоугольника.
23. Неразветвленная цепь составлена из двух катушек: у первой катушки индуктивность 
и сопротивление 
, у второй катушки индуктивность 
и сопротивление 
.
Определить ток в цепи и напряжения на каждой катушке, а также построить в масштабе векторную диаграмму, если частота f=50 Гц и приложенное напряжение U=12,6 В.
Решение:
Индуктивное сопротивление первой катушки
т. е. оно численно равно активному сопротивлению 
, что обусловливает отставание тока по фазе от напряжения на 1/8 периода (на 45°).
Действительно, тангенс угла сдвига фаз
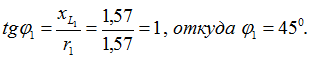
Индуктивное сопротивление второй катушки
Так как ее активное сопротивление 
то тангенс угла сдвига фаз
Построим в масштабе треугольник сопротивлений для рассматриваемой цепи. Для этого зададимся масштабом сопротивлений 
. Тогда на диаграмме сопротивление 1,57 Ом будет изображено отрезком 15,7 мм, сопротивление 2,7 Ом — отрезком 27 мм и т. д. На рис. 27 отрезок, изображающий активное сопротивление 
, отложен в горизонтальном направлении, а отрезок, изображающий индуктивное сопротивление 
, — в вертикальном направлении под прямым углом к 
.
Полное сопротивление 
первой катушки является гипотенузой прямоугольного треугольника. Из вершины с этого треугольника в горизонтальном направлении отложен отрезок, изображающий сопротивление 
, и под прямым углом к нему вверх — отрезок, изображающий сопротивление 
. Гипотенуза се прямоугольного треугольника означает полное сопротивление 
второй катушки.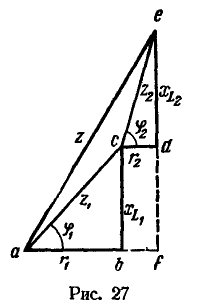
Из рис. 27 видно, что отрезок ае, изображающий полное сопротивление z неразветвленной цепи из двух катушек, не равен сумме отрезков ас и се, т. е. 
. Чтобы определить полное сопротивление z рассматриваемой цепи, следует сложить отдельно активные (
, отрезок аf) и индуктивные (
, отрезок ef) сопротивления катушек.
Гипотенуза ае, означающая полное сопротивление z цепи, определяется по теореме Пифагора:
Ток в цепи определяется по закону Ома:
Напряжение на первой катушке
Напряжение на второй катушке
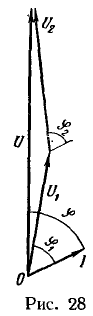
Строим векторную диаграмму (рис. 28), приняв масштабы:
а) для тока 
; тогда вектор тока изобразится отрезком длиной 25 мм;
б) для напряжения 
; при этом вектор напряжения 
будет иметь длину 55,2 мм, вектор напряжения 
— длину 71 мм, а вектор приложенного напряжения 
— длину 126 мм.
Начало вектора 
совмещено с концом вектора 
для возможности сложения векторов напряжений но правилу многоугольника (напряжение, приложенное к неразветвленной цепи катушек, равно геометрической сумме напряжений отдельных катушек).