Расчет переходных процессов в цепях второго порядка
1. Цепь (рис. 8.26, а) включается на постоянное напряжение U=125 В. Найти выражение напряжения на конденсаторе для трех случаев: 1) R=250 Ом, L=667 мГн, С=2мкФ; 2) R=100 Ом, L=40 мГн, С=1 мкФ; 3) R=100 Ом, L=40мГн, С=5мкФ.
Решение:
Наметим план решения задачи. Напряжение на конденсаторе находим в виде суммы установившегося и свободного значений
![]()
Установившееся значение напряжения на конденсаторе равно нулю (![]() ), так как при установившемся режиме конденсатор шунтирован индуктивностью катушки накоротко.
), так как при установившемся режиме конденсатор шунтирован индуктивностью катушки накоротко.
Для нахождения вида решения свободной составляющей составим характеристическое входное сопротивление цепи и приравняем его нулю
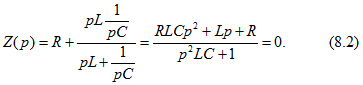
Это уравнение второго порядка и, следовательно, оно имеет два корня
![]()
Для каждого из трех заданных случаев по уравнению (8.3) определим вид корней (действительные разные, действительные кратные или комплексно-сопряженные) и в соответствии с ним найдем свободное решение ![]() по одной из формул. Заметим, что свободная составляющая напряжения на конденсаторе содержит две постоянные интегрирования.
по одной из формул. Заметим, что свободная составляющая напряжения на конденсаторе содержит две постоянные интегрирования.
Для определения постоянных интегрирования поступим так. Составим уравнения по законам Кирхгофа:
![]()
Запишем независимые начальные условия
![]()
Подставим их в уравнения (8.4) для начального момента времени (после коммутации):
![]()
Решив их, находим ![]() . Затем, используя зависимость
. Затем, используя зависимость ![]() для момента
для момента ![]() , получим
, получим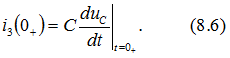
Наконец, определим две неизвестные постоянные интегрирования из уравнения (8.1), в которое подставляем найденные ![]() и из уравнения (8.6).
и из уравнения (8.6).
Конкретное применение указанной методики расчета рассмотрим для каждого из трех заданных случаев.
1. Подставим в уравнение (8.3) числовые значения первого случая
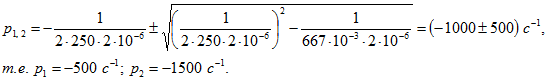
Получены корни действительные и различные, следовательно, свободная составляющая напряжения на конденсаторе
![]()
Далее из уравнений (8.5) с учетом начальных условий (I) и (II) получим
![]()
Решая эту систему уравнений, находим ![]() . Подставив в равенство (8.1) и в выражение тока
. Подставив в равенство (8.1) и в выражение тока ![]() уравнение (8.7), получим
уравнение (8.7), получим
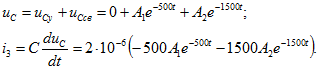
Перепишем эти уравнения для момента ![]() и затем, подставляя в них
и затем, подставляя в них ![]() , получим
, получим![]()
Отсюда ![]() . Таким образом, согласно (8.1) и (8.7) искомое напряжение
. Таким образом, согласно (8.1) и (8.7) искомое напряжение
![]()
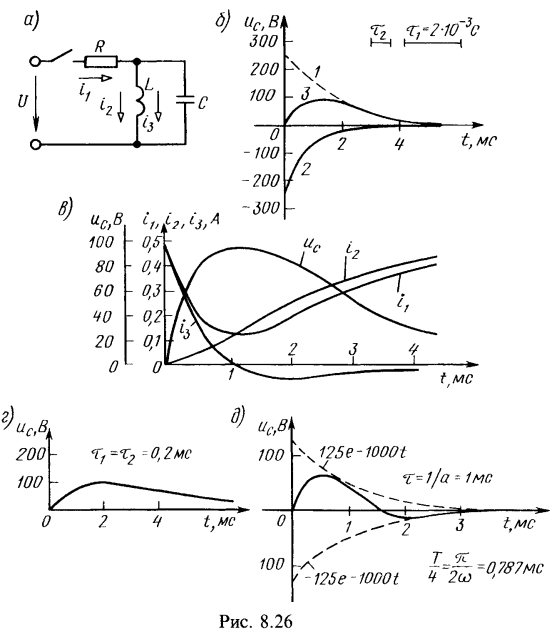
Графики отдельных составляющих решения и суммарного значения напряжения на конденсаторе построены на рис. 8.26, б: на нем кривая: ![]() .
.
Для упражнения вычислим также все токи и построим их графики
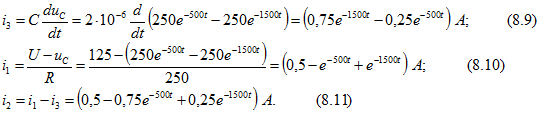
Результаты расчетов приведены в табл. 1; ![]() принято равным
принято равным ![]()
Таблица 1
| 0 | 0,5 | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 | 4,0 |
| 0,5 | 0,194 | 0,116 | 0,131 | 0,185 | 0,236 | 0,239 | 0,33 | 0,368 |
| 0 | 0,034 | 0,10 | 0,17 | 0,24 | 0,29 | 0,34 | 0,37 | 0,40 |
| 0,5 | 0,16 | 0,016 | -0,039 | -0,055 | -0,054 | -0,047 | -0,04 | -0,032 |
| 0 | 76,6 | 95,9 | 91,7 | 79,5 | 65,7 | 53,0 | 42,1 | 33,2 |
Графики токов и напряжения даны на рис. 8.26, в.
2. Подставим в формулу (8.3) числовые значения второго случая:
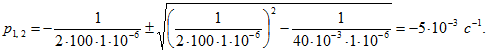
Корень — двукратный, следовательно, решение ищем в виде
![]()
Далее, как и в нервом случае, из уравнений (8.5) с учетом начальных условий (I) и (II) найдем ![]() .
.
Подставив в уравнение (8.1) и в выражение ![]() уравнение (8.12), получим
уравнение (8.12), получим
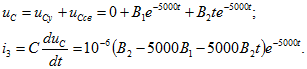
Переписывая эти уравнения для момента ![]() и подставляя в них
и подставляя в них ![]() , получим
, получим ![]()
Следовательно, ![]() . Таким образом, искомое напряжение согласно (8.1) и (8.12)
. Таким образом, искомое напряжение согласно (8.1) и (8.12) ![]()
Результаты расчетов приведены в табл. 2.
Таблица 2
| 0 | 0,5 | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 | 4,0 |
| 0 | 48,7 | 75,8 | 88,6 | 92,0 | 89,5 | 83,7 | 76,0 | 67,7 |
График напряжения ![]() построен на рис. 8.26, г.
построен на рис. 8.26, г.
3. Рассмотрим третий случай числовых значений параметров схемы рис. 8.26, а.
Подставляя эти значения в уравнение (8.3), находим
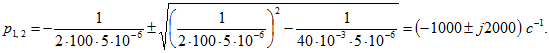
Корни характеристического уравнения образуют комплексно-сопряженную пару чисел ![]() , следовательно, свободную составляющую напряжения на конденсаторе следует искать в виде
, следовательно, свободную составляющую напряжения на конденсаторе следует искать в виде
![]()
По аналогии с предыдущими случаями из уравнений (8.5) с учетом начальных условий (I) и (II) получим ![]() .
.
Подставив в (8.1) и в выражение ![]() уравнение (8.13), получим
уравнение (8.13), получим
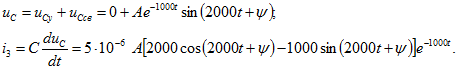
Переписывая эти уравнения для момента ![]() и подставляя в них
и подставляя в них ![]() , получим
, получим ![]() .
.
Решая их, находим ![]() . Таким образом, согласно (8.1) и (8.13) искомое напряжение
. Таким образом, согласно (8.1) и (8.13) искомое напряжение ![]() .
.
Результаты расчетов приведены в табл. 3.
График напряжения построен на рис. 8.26, д.
Таблица 3
| 0 | 0,5 | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 | 4,0 |
| 0 | 63,8 | 41,8 | 3,9 | -12,8 | -9,8 | -1,7 | 2,5 | 2,3 |
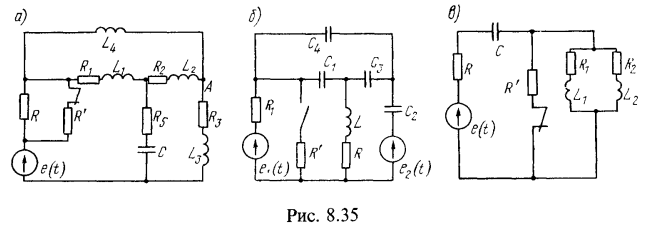
2. Для каждой из схем рис. 8.35, а — в определить (не составляя уравнений) степень n характеристического уравнения, описывающего свободный процесс после соответствующей коммутации. Дополнительные условия для схемы (рис. 8.35,в): ![]() .
.
Решение:
Как известно из теории, степень характеристического уравнения, описывающего переходные процессы, равна числу независимых начальных условий в послекоммутационной схеме цепи.
Рассмотрим схему рис. 8.35, а. Она содержит пять реактивных элементов, которые определяют четыре начальных значения тока, протекающих через индуктивные катушки, и одно начальное значение напряжения на конденсаторе. Однако не все эти пять начальных значений являются независимыми. Определим число основных независимых начальных условий. Так, например, если в качестве основных независимых начальных условий принять значения токов, протекающих через ![]() , то ток через
, то ток через ![]() будет не основным, ибо его начальное значение определяется первым законом Кирхгофа, примененным к узлу А. Таким образом, схема рис. 8.35, а содержит четыре независимых начальных условия, а следовательно, характеристическое уравнение будет иметь порядок (n=4).
будет не основным, ибо его начальное значение определяется первым законом Кирхгофа, примененным к узлу А. Таким образом, схема рис. 8.35, а содержит четыре независимых начальных условия, а следовательно, характеристическое уравнение будет иметь порядок (n=4).
В схеме рис. 8.35, б пять реактивных элементов, однако число независимых начальных условий равно трем. Если, например, в качестве основных принять начальные значения напряжений на конденсаторах ![]() , то из второго закона Кирхгофа, примененного к контуру, состоящему из
, то из второго закона Кирхгофа, примененного к контуру, состоящему из ![]() , напряжение на конденсаторе
, напряжение на конденсаторе ![]() будет их следствием. Аналогично из рассмотрения уравнения Кирхгофа, составленного для контура
будет их следствием. Аналогично из рассмотрения уравнения Кирхгофа, составленного для контура ![]() можно установить, что напряжение на конденсаторе
можно установить, что напряжение на конденсаторе ![]() не является независимым условием. Итак, n=3.
не является независимым условием. Итак, n=3.
В схеме рис. 8.35, в три реактивных элемента, но число основных независимых условий равно двум. Это определяется подобием параллельных ветвей ![]() , эквивалентное сопротивление которых имеет не второй, а первый порядок, и поэтому характеристическое сопротивление всей схемы имеет второй порядок (n=2).
, эквивалентное сопротивление которых имеет не второй, а первый порядок, и поэтому характеристическое сопротивление всей схемы имеет второй порядок (n=2).