Закон Кулона
1 Два одинаковых точечных заряда q взаимодействуют в вакууме с силой F=0,1 Н. Расстояние между зарядами r = 6 м. Найти эти заряды.
Решение:
По закону Кулона 
, где 
2 Какое число N электронов содержит заряд в одну единицу заряда в системе единиц СИ (1 Кл)? Элементарный заряд 
Решение: 
электронов.
3 Два точечных заряда q1 и q2 находятся на расстоянии r друг от друга. Если расстояние между ними уменьшается на величину Δr = 50 см, то сила взаимодействия F увеличивается в два раза. Найти расстояние r.
Решение:
4 Тонкая шелковая нить выдерживает максимальную силу натяжения Т=10 мН. На этой нити подвешен шарик массы m = 0,6 г, имеющий положительный заряд q1 = 11 нКл. Снизу в направлении линии подвеса к нему подносят шарик, имеющий отрицательный заряд q2= -13 нКл. При каком расстоянии r между шариками нить разорвется?
Решение:
5 Отрицательный точечный заряд Q расположен на прямой, соединяющей два одинаковых положительных точечных заряда q. Расстояния между отрицательным зарядом и каждым из положительных относятся между собой, как 1:3. Во сколько раз изменится сила, действующая на отрицательный заряд, если его поменять местами с ближайшим положительным?
Решение:
Положительные заряды q могут быть расположены как по обе стороны от отрицательного заряда Q, так и по одну сторону от него. Отношение сил в первом и втором случаях: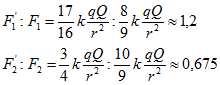
где r – расстояние от заряда Q до ближайшего положительного заряда q.
6 Два отрицательных точечных заряда q1 = — 9 нКл и q2= — 36 нКл расположены на расстоянии r=3м друг от друга. Когда в некоторой точке поместили заряд q0, то все три заряда оказались в равновесии. Найти заряд q0 и расстояние между зарядами q1 и q0.
Решение:
Обозначим модуль силы буквой F с двумя индексами, первый из которых показывает, на какой заряд действует сила, а второй со стороны какого заряда она действует (например, F01–сила, действующая на заряд q0 со стороны заряда q1). Возьмем в качестве координатной оси ОХ прямую, проходящую через заряды q1 и q2 (рис. 324). За начало отсчета О примем точку, где находится заряд q1 а за положительное направление от заряда q1 к заряду q2. Закон Кулона (в нашей записи) дает возможность определить лишь модуль вектора силы, а знак проекции вектор будет, как обычно, положительным, если сила направлена в положительном направлении оси ОХ, и отрицательным в противном случае.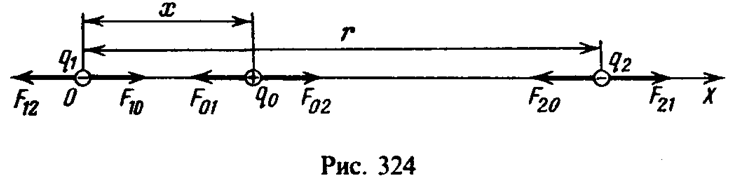
На каждый из трех зарядов действуют со стороны двух других по две силы. Для равновесия необходимо, чтобы эти две силы были противоположными по направлению. Легко видеть, что это условие выполняется лишь в случае, когда заряд q0 находится на оси ОХ между зарядами q1 и q2 и имеет противоположный по сравнению с q1, и q2 знак. Пусть расстояние между зарядами q1 и q0 равно х (0<х<r). Тогда (рис. 324):
а) на q0 действуют силы
б) на q1 действуют силы
в) на q2 действуют силы
При равновесии всех трех зарядов:
а)–F01+F02 = 0; б) -F12 + F10 = 0; в) F21-F20 = 0.
Условие а) приводит к квадратному уравнению относительно х:
Для корней этого уравнения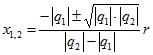
выполняются условия: 0<x1x2<0 при |q2| > |q1|; x2>r при |q2| < |q1|. Второй корень должен быть отброшен, как не удовлетворяющий условиям равновесия. Таким образом.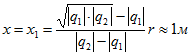
Условие б) дает 
отсюда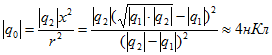
7 Три одинаковых точечных заряда q = 20 нКл расположены в вершинах равностороннего треугольника. На каждый заряд действует сила F=10mH. Найти длину а стороны треугольника.
Решение:
Каждый заряд q взаимодействует с двумя другими зарядами q, расположенными на расстоянии а от рассматриваемого (рис. 325).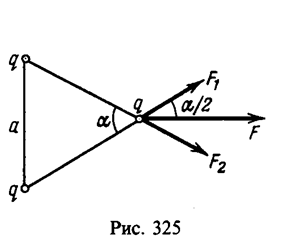
Поэтому на любой заряд действуют две равные по модулю силы 
. Равнодействующая этих сил (проекция векторной суммы этих сил на диагональ параллелограмма)
; отсюда 
8 Три одинаковых точечных заряда q1=q2 =q3 = 9 нКл расположены в вершинах равностороннего треугольника. Какой точечный заряд q0 нужно поместить в центре треугольника, чтобы система находилась в равновесии?
Решение:
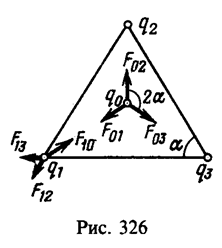
На заряд q1 действуют две равные по модулю силы со стороны зарядов q2 и q3, а также сила со стороны заряда q0 (рис.326). Ввиду равенства зарядов q1=q2=q3 = q получаем 
. На заряд q0 действуют три равные по модулю силы, равнодействующая которых равна нулю.
9 Четыре одинаковых точечных заряда q=10 нКл расположены в вершинах квадрата со стороной a=10см. Найти силу, действующую со стороны трех зарядов на четвертый.
Решение:
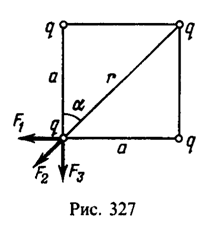
Каждый заряд q взаимодействует с тремя другими зарядами q, два из которых находятся на расстоянии а от рассматриваемого, а один – на расстоянии 
(рис. 327). Поэтому на любой заряд действуют три силы: 
. Равнодействующая этих сил (проекции векторной суммы этих сил на диагональ квадрата)
и направлена по диагонали квадрата от его центра.
10 Четыре одинаковых по модулю точечных заряда | q | = 20 нКл, два из которых положительны, а два отрицательны, расположены в вершинах квадрата со стороной а = 20 см так, как показано на рис. 69. Найти силу, действующую на помещенный в центре квадрата положительный точечный заряд q0 = 20 нКл.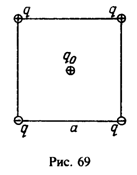
Решение: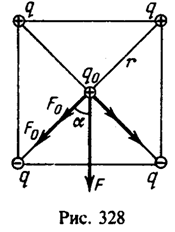 
На заряд q0 действуют четыре силы, направленные попарно по двум диагоналям квадрата (рис. 328) и равные по модулю 
(
-половина диагонали квадрата). Равнодействующая этих сил
где 
–угол между диагональю и направлением равнодействующей.
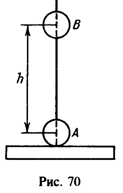
11 На изолированной подставке расположен вертикально тонкий фарфоровый стержень, на который надет металлический полый шарик А радиуса r (рис. 70). После сообщения шарику заряда q = 60 нКл по стержню опущен такой же незаряженный металлический шарик в массы m = 0,1 г, который соприкасается с шариком А. На каком расстоянии h от шарика А будет находиться в равновесии шарик в после соприкосновения, если 
? Трением шариков о стержень пренебречь.
Решение:
После соприкосновения шарика В с шариком А заряд q перераспределится между шариками поровну и шарик В будет подниматься вверх. Равновесие силы тяжести и силы Кулона наступит при 
; отсюда h=9 см.
12 Вокруг отрицательного точечного заряда q0=-5 нКл равномерно движется по окружности под действием силы притяжения маленький заряженный шарик. Чему равно отношение заряда шарика к его массе, если угловая скорость вращения шарика ω = 5 рад/с, а радиус окружности R = 3 см?
Решение:
13 Два одинаковых шарика массы т = 9 г находятся друг от друга на расстоянии r, значительно превышающем их размеры. Какие равные заряды необходимо поместить на шариках, чтобы сила их кулоновского взаимодействия уравновешивала силу гравитационного притяжения?
Решение:
, где 
-гравитационная постоянная.
14 Найти силы взаимодействия двух точечных зарядов q1 =4 нКл и q2=6 нКл в вакууме и в керосине (диэлектрическая проницаемость e = 2) на расстоянии r = 20 см.
Решение:
Силы взаимодействия зарядов в вакууме и в керосине 
.
Следует отметить, что силы, приложенные к различным по модулю зарядам, равны по модулю и противоположны по направлению. На экзаменах нередко ошибаются, утверждая, что к большему заряду приложена большая сила. Это противоречит не только закону Кулона, но и третьему закону Ньютона.
15 Два точечных заряда, находясь в воздухе на расстоянии r1 = 5 см, взаимодействуют друг с другом с силой F1 = 120мкН, а находясь в некоторой непроводящей жидкости на расстоянии r2 = 10см, – с силой F2=15мкH. Какова диэлектрическая проницаемость жидкости?
Решение:
16 Найти расстояние r1 между двумя одинаковыми точечными зарядами, находящимися в масле (диэлектрическая проницаемость ? = 3), если сила взаимодействия между ними такая же, как в вакууме на расстоянии r2 = 30 см.
Решение:
17 Два одинаковых заряженных шарика, подвешенных на нитях равной длины в одной точке, разошлись в воздухе на некоторый угол 2α. Какова должна быть плотность ρ материала шариков, чтобы при погружении их в керосин (диэлектрическая проницаемость ε = 2) угол между нитями не изменился? Плотность керосина 
Решение: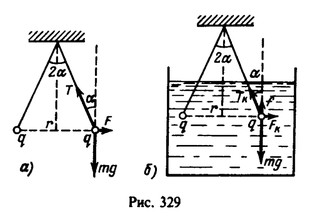 
До погружения в керосин на шарики действуют (рис. 329, а): сила тяжести mg, сила натяжения нити Т, сила кулоновского отталкивания 
, где m — масса шарика, q — его заряд и r – расстояние между шариками. При равновесии шарика суммы проекций сил на вертикальное и горизонтальное направления равны нулю:
(1)
При погружении шариков в керосин сила Кулона 
; сила Архимеда 
и направлена вверх (рис. 329,б).
Условие равновесия сил теперь примет вид
(2)
Из (1) и (2) имеем
отсюда 
18 Два одинаковых заряженных шарика подвешены на нитях равной длины в одной точке и погружены в жидкость. Плотности материала шариков и жидкости равны ρ и ρж. При какой диэлектрической проницаемости жидкости угол расхождения нитей в жидкости и в воздухе будет один и тот же?
Решение:
(см. задачу 17).
19 Одноименные точечные заряды q1 и q2 расположены в вершинах равностороннего треугольника со стороной r в однородной среде с диэлектрической проницаемостью ε. Найти суммарную силу F, действующую на точечный заряд q3, расположенный в третьей вершине треугольника.
Решение:
20 Три точечных заряда, расположенных друг от друга на расстояниях r12, r13 и r23, взаимодействуют в вакууме с силами F12, F13 и F23 соответственно. Найти через известные величины выражение для третьего заряда.
Решение:
Обозначим заряды через q1, q2 и q3. Тогда по закону Кулона
Исключая из этих уравнений q1 и q2, найдем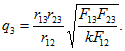
21 С какой силой взаимодействовали бы в вакууме два одинаковых точечных заряда q=1Кл, находясь на расстоянии r = 0,5 км друг от друга?
Решение:
Сила взаимодействия 
. Эта сила довольно велика: она приблизительно равна силе, с которой притягивается к Земле тело массы m = 3600 кг.
22 Два одинаковых шарика подвешены в воздухе на нитях так, что их поверхности соприкасаются. После того как каждому шарику был сообщен заряд q = 0,4 мкКл, шарики разошлись на угол 2α = 60°. Найти массу шариков, если расстояние от центров шариков до точки подвеса l=0,2 м.
Решение: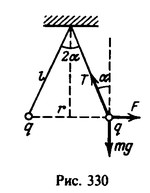 
На каждый шарик действуют: сила натяжения нити Т, сила тяжести mg и сила кулоновского отталкивания 
, где 
(рис. 330). При равновесии шарика суммы проекций сил на вертикальное и горизонтальное направления равны нулю (см. задачу 17):
Исключив из этих уравнений Т и учитывая выражения для F и r, получим
23 Составлен прибор из двух одинаковых проводящих шариков массы m = 15 г, один из которых закреплен, а другой подвешен на нити длины l=20 см. Шарики, находясь в соприкосновении, получают одинаковые заряды, вследствие чего подвижный шарик отклоняет нить на угол 2α = 60° от вертикали. Найти заряд каждого шарика.
Решение: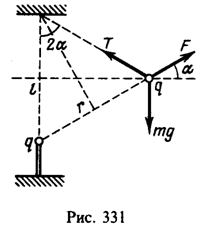 
На подвижный шарик действуют: сила тяжести mg, сила кулоновского отталкивания F и сила натяжения нити Т (рис. 331). При равновесии шарика суммы проекций сил на горизонтальное и вертикальное направления равны нулю:
Fcosα – Tsin2α=0,
Fsinα+ T cos2α — mg=0.
Исключая из этих уравнений T находим
Используя известную формулу 
, получаем
Как видно из рис. 331, расстояние между шариками r=2lsina.
Следовательно, 
Отсюда
24 Шарик, несущий заряд q = 50 нКл, коснулся внутренней поверхности незаряженной проводящей сферы радиуса R= 20 см. Найти поверхностную плотность заряда на внешней поверхности сферы.
Решение:
Заряд шарика q полностью перейдет на внешнюю поверхность сферы и распределится по ней равномерно. Поэтому поверхностная плотность заряда на сфере 
.
25 Найти поверхностную плотность заряда на внешней поверхности проводящей сферы радиуса R = 20 см, если в центре сферы на изолирующей палочке находится шарик, несущий заряд q= 50нКл. Будет ли изменяться поверхностная плотность при изменении положения шарика внутри сферы?
Решение: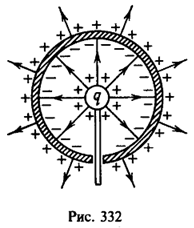 
При внесении шарика с зарядом q внутрь проводящей сферы на внешней поверхности сферы появляются индуцированные заряды того же знака, что и заряд q, а на внутренней – противоположного знака (рис. 332). Поверхностная плотность заряда на сфере
При изменении положения шарика электрическое поле внутри сферы будет меняться, но это не скажется на распределении зарядов на внешней поверхности сферы и их плотность будет прежней.